objectGeometry.py

W niniejszym pliku zawarte zostały wszystkie funkcje które zostały użyte w celu określenia położenia poszczególnych punktów wirnika. Podczas tej procedury wykorzystany został moduł SymPy.

objectGeometry.obliczWymaganeParametry(Goniec)

Funkcja mająca na celu określenie położenia punktów głównych wirnika. Są to między innymi punkty określające przekrój poprzeczny wirnika, zakrzywienie łopatki, oraz zaokrąglenie w górnej części konstrukcji.

Parametry:Goniec (Sender) – obiekt Gońca zawierający informacje wymagane w przygotowaniu analizy numerycznej.
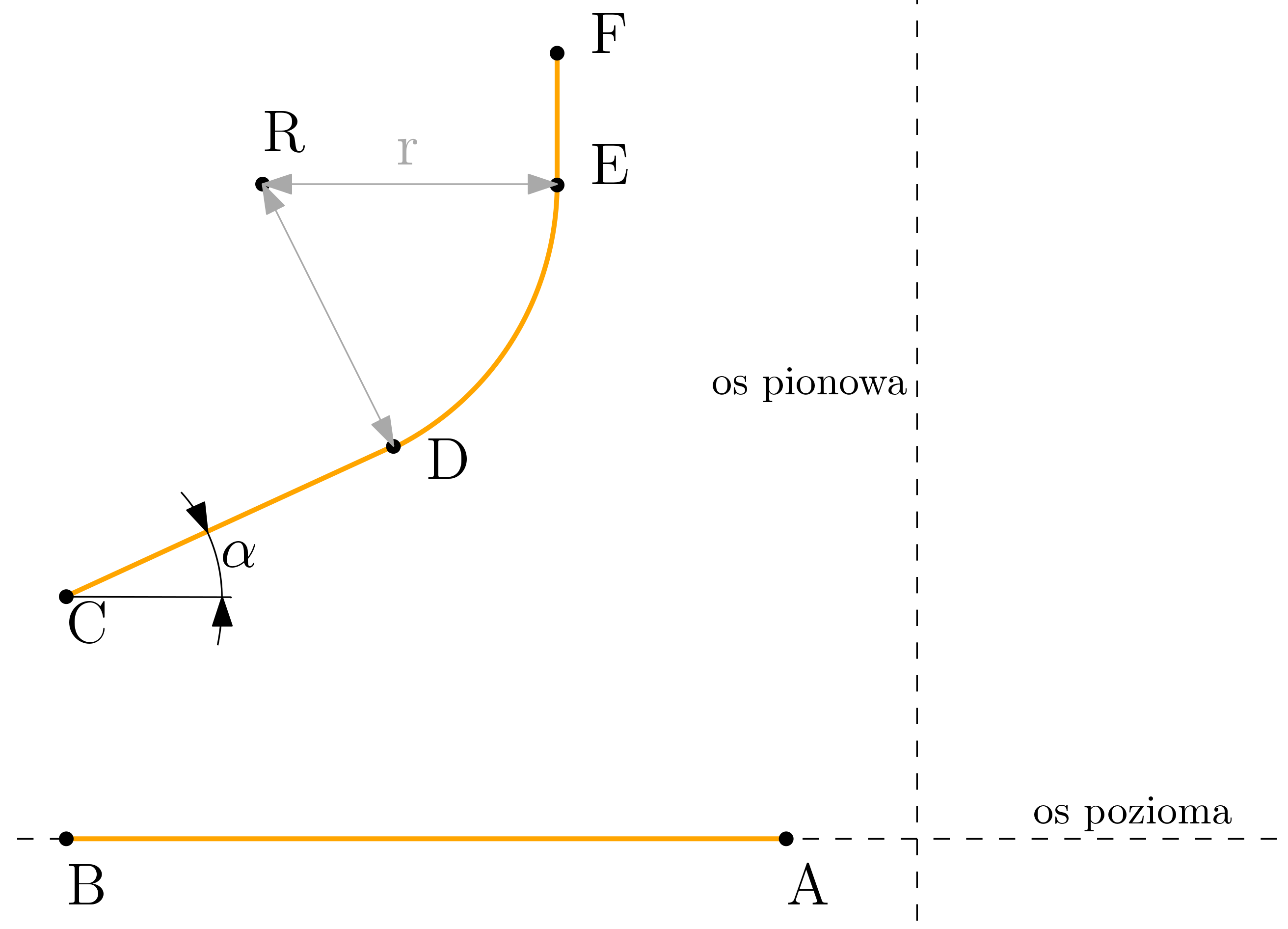
objectGeometry.wspolrzednePktPrzekroju(geometria, temp)

Funkcja służąca do obliczenia niezbędnych wymiarów wirnika. Na poniższym rysunku został przedstawiony przekrój wirnika i punkty określające jego wymiary.

Szkic przekroju wirnika

Szkic przekroju wirnika

Punkty te odpowiadają następującym wymiarowm pobranym z GUI:

  • Promień otworu - odl. od osi pionowej do punktu A
  • Promień zewnętrzny - odl. od osi pionowej do punktu B
  • Promień u wylotu - odl. od osi pion
  • Wysokość łopatki - odcinek \(|BC|\)
  • Kąt alfa - kąt \(\alpha\)
  • Promień zaokrąglenia - odcinek \(|RD|=|RE|\)
  • Wysokość pod naddatek - odcinek \(|EF|\)
  • Wysokość wirnika - odległość od punktu F do osi poziomej.

W celu stworzenia geometrii w programie GMSH należy obliczyć położenie punktu \(D\). Punkt ten jest określane poprzez sprawdzenie punktów wspólnych okręglu zakreślonego w punkcie \(R\) o promieniu \(|RD|\) z prostą przechodzącą przez punkt \(C\) odchyloną od poziomu o kąt \(\alpha\). Zadanie to zostało wykonane przy użyciu modułu SymPy.

Parametry:
  • geometria (Geometry) – obiekt klasy Geometry zawierający dane geometryczne wirnika
  • temp (dictionary) – tymczasowy kontener na dane, użyty w celu przechowywania informacji.
Return temp:

uaktualniony kontener na dane.
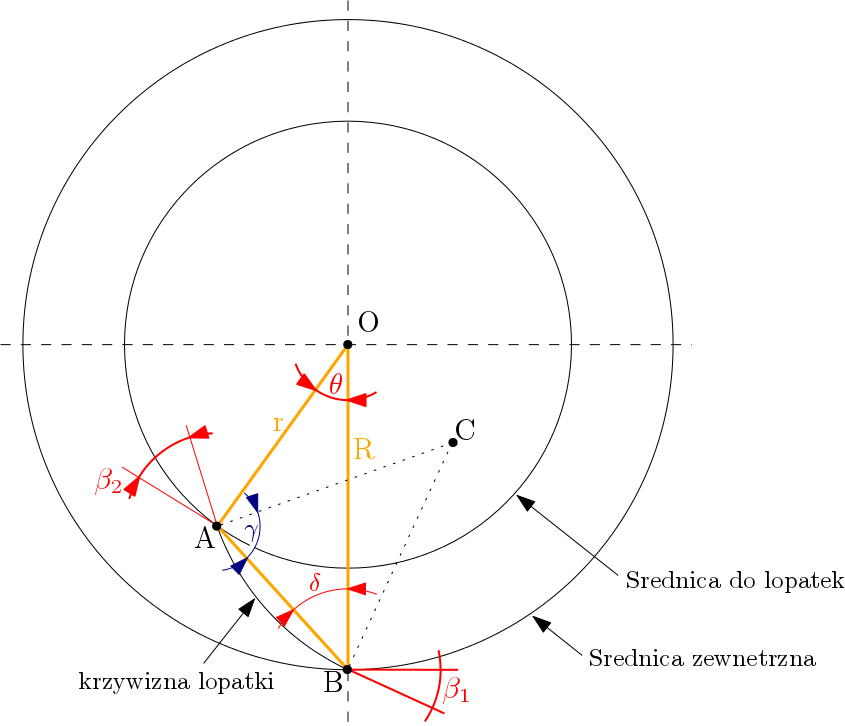
objectGeometry.obliczPunktyKrzywej(geometria)

Funkcja obliczająca wspołrzędne punktów A, B, C łopatki. Algorytm wykorzystuje funckcję fsolve z modułu SciPy w celu rozwiązania równania nieliniowego przedstawionego poniżej. W oparciu o współrzędne wymienionych punktów funkcja dodajWspolrzedne() oblicza osiem punktów leżących na krzywiźnie łopatki.

Położenie łopatki

Szkic wirnika w płaszczyźnie XY

W celu określenia współrzędnej punktu \(A\) należy wpierw określić kąt \(\theta\). Kąt można określić następującą zależnością:

\[\begin{split}\delta = \arctan(\tfrac{r-sin\theta}{R-rsin\theta}) \\ \gamma = \delta + {\beta}_{1} \\ \gamma + {\beta}_{2} + \theta + \delta = 180^{\circ} \implies {\beta}_{1} + {\beta}_{2} + \theta + 2\cdot\delta = 180^{\circ}\end{split}\]
\[{\beta}_{1} + {\beta}_{2} + \theta + 2\arctan(\tfrac{r-sin\theta}{R-rsin\theta}) - 180^{\circ} = 0\]
Parametry:geometria (Geometry) – obiekt klasy Geometry zawierający dane geometryczne wirnika
Return pktyLopatki:
 tablica zawierająca punkty znajdujące się na krzywej łopatki.
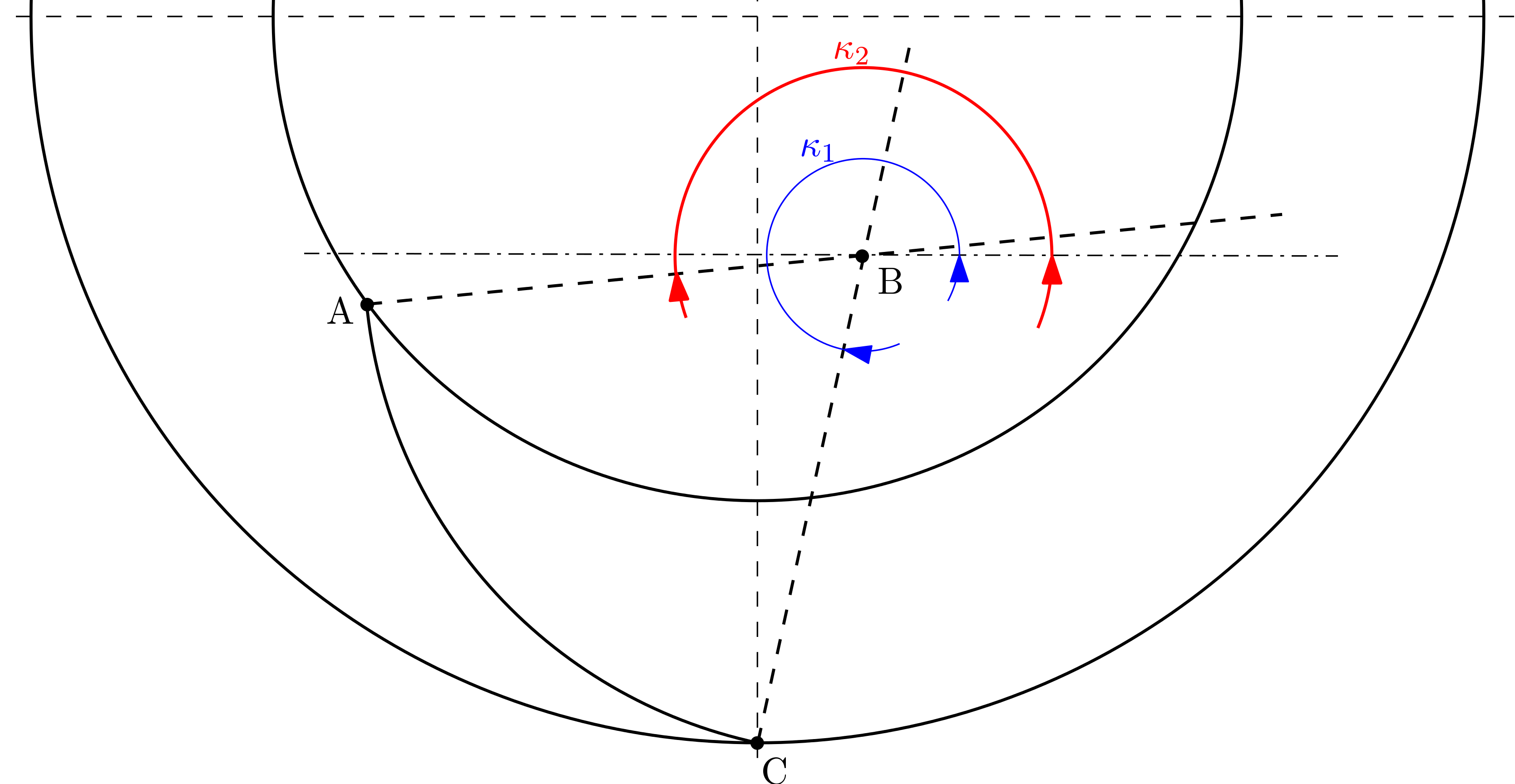
objectGeometry.dodajWspolrzedne(wek)

Funkcja zawiera opis krzywizny łopatki we współrzędnych parametrycznych. W pierwszym etapie zostają wyznaczone kąty \({\kappa}_{1}\) i \({\kappa}_{2}\). Następnie tworzona jest tablica zawierająca osiem równoodległych wartości z pomiędzy tych kątów. Tak otrzymane dane zostają użyte przy określaniu punktów leżących na krzywej \(AC\).

Krzywizna łopatki

Szkic krzywizny łopatki

Parametry:wek (lista zawierająca współrzędne punktów na krzywiźnie łopatki) – tablica zawierająca położenie punktów \(A\), \(B\) i \(C\).
objectGeometry.policzPktyZaokraglenia(geometria, temp)

Funkcja ma na celu obliczenie punktów na krzywej wirnika w górnej jego części (zob. krzywą \(ED\) na rysunku przekroju wirnika). Procedura obliczania punktów na krzywej jest identyczna jak w przypadku funkcji dodajWspolrzedne().

Parametry:
  • geometria (Geometry) – obiekt klasy Geometry zawierający dane geometryczne wirnika
  • temp (dictionary) – tymczasowy kontener na dane, użyty w celu przechowywania informacji.
Return kolo_BC:

obiekt list zawierający punkty leżące na zaokrągleniu w górnej części wirnika.